Scacchiera di Adelson
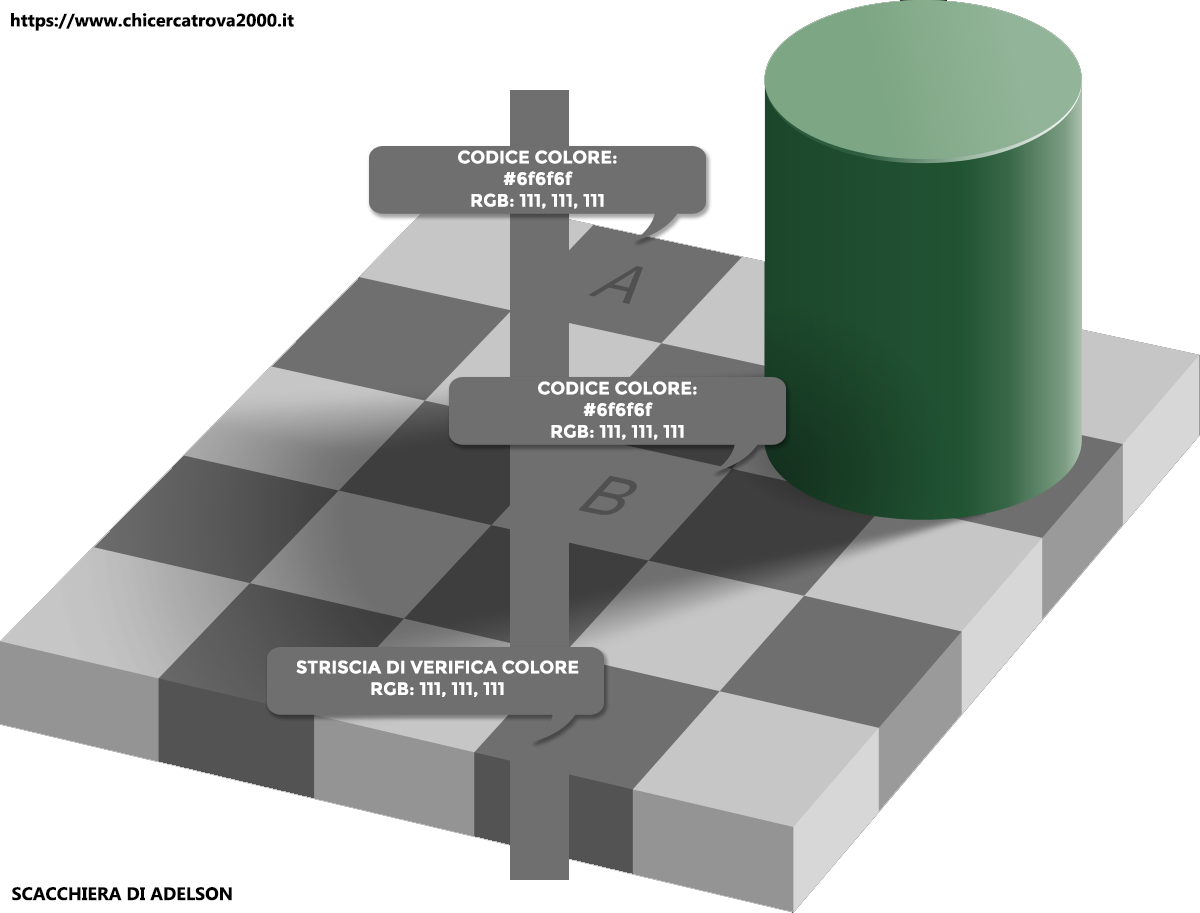
Si chiama “scacchiera di Adelson”.
Questa illusione, creata da Edward Howard Adelson, raffigura una scacchiera con una serie di quadrati bianchi e neri: in particolar modo si possono notare due quadrati A e B. Apparentemente sembrano di colori diversi, A sembra più scuro di B, ma in realtà sono dello stesso colore (Il colore è codificato come #6F 6F 6F nella modalità RGB Esadecimale). Perché ci appaiono di colori differenti? A causa dell’ombra creata dal cilindro verde. Una superficie bianca in ombra riflette meno luce di una superficie nera in piena luce, dunque due quadrati identici con un’illuminazione differente ci appaiono come diversi.
E’ l’ennesima dimostrazione che il nostro cervello interpreta ciò che vede e spesso porta alla nostra percezione cose che non sono reali.
Il nostro cervello in modo automatico “capisce” che B si trova in una casella che deve “per forza” essere bianca e quindi “conclude” che anche se l’ombra del cilindro scurisce la casella, essa sarà comunque bianca (anche se un po’ più scuretta) e non certo del colore della casella A e così ce la fa percepire.
Ma se provate ad usare un color grabber in questa immagine avrete lo stesso codice colore di entrambe le caselle.
Perché accade?
E’ solo l’ennesima dimostrazione che il nostro cervello “interpreta ciò che vede usando vari meccanismi sviluppati durante la nostra evoluzione” e non si limita a farci arrivare alla coscienza l’immagine nuda e cruda come è ma come si aspetta che sia, e ciò spesso porta alla nostra percezione cose che non sono reali.
Il nostro cervello in modo automatico “capisce” che B si trova in una casella che deve “per forza” essere bianca e quindi “conclude” che anche se l’ombra del cilindro scurisce la casella, essa sarà comunque bianca (anche se un po’ più scuretta) e non certo del colore della casella A e così ce la fa percepire.
Ma se provate ad usare un color grabber su questa immagine avrete lo stesso codice colore in entrambe le caselle.